Sparse Networks with Overlapping Communities (SNetOC) package: demo_overlappingcommunity
This Matlab script finds overlapping communities in a network of political blogs, using the wrapper function overlapping_community_detection.m. For a full analysis of this dataset, see the Matlab demo demo_polblogs.m.
For downloading the package and information on installation, visit the SNetOC webpage.
Reference:
- A. Todeschini, X. Miscouridou and F. Caron (2017) Exchangeable Random Measures for Sparse and Modular Graphs with Overlapping Communities. arXiv:1602.02114.
Authors:
- A. Todeschini, Inria
- X. Miscouridou, University of Oxford
- F. Caron, University of Oxford
Tested on Matlab R2017a. Requires the Statistics toolbox.
Last Modified: 01/2020
Contents
close all clear all % Add path addpath ./GGP/ ./CGGP/ ./utils/
Load network of political blogs
Data can be downloaded from here.
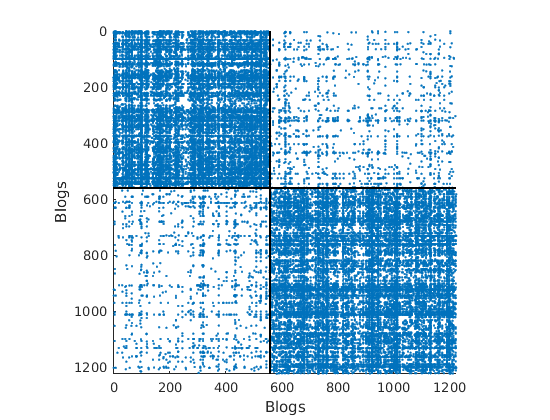
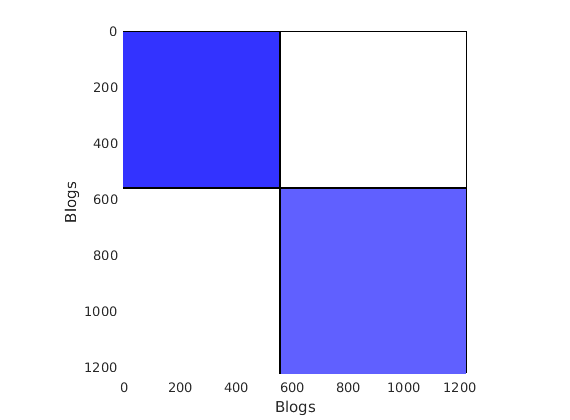
load ./data/polblogs/polblogs.mat titlenetwork = 'Political blogosphere Feb. 2005'; name = 'polblogs'; labels = {'Blogs', 'Blogs'}; groupfield = 'name'; % meta field displayed for group plot % Transform the graph to obtain a simple graph G = Problem.A | Problem.A'; % make undirected graph G = logical(G-diag(diag(G))); % remove self edges (#3) % Collect metadata meta = struct; meta.name = cellstr(Problem.aux.nodename); meta.source = cellstr(Problem.aux.nodesource); meta.isright = logical(Problem.aux.nodevalue); meta.degree = num2cell(full(sum(G,2))); meta.groups = zeros(size(meta.isright)); meta.groups(~meta.isright) = 1; meta.groups(meta.isright) = 2; color_groups = [0 0 .8; .8 0 0]; label_groups = {'Left', 'Right'}; fn = fieldnames(meta); % Remove nodes with no edge (#266) ind = any(G); G = G(ind, ind); for i=1:length(fn) meta.(fn{i}) = meta.(fn{i})(ind); end % Plot adjacency matrix (sorted) figure('name', 'Adjacency matrix (sorted by ground truth political leaning)') spy(G); xlabel(labels{2}) ylabel(labels{1})
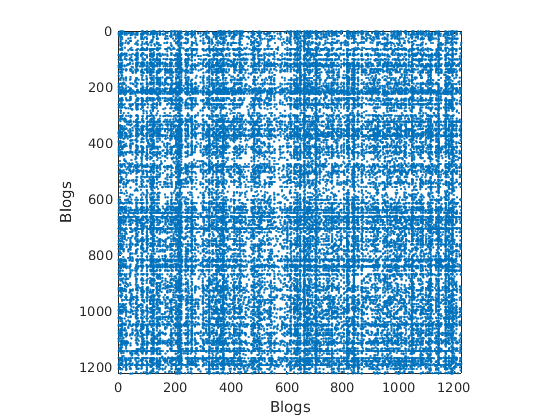
% Shuffle nodes: irrelevant due to exchangeability, just to check we do not cheat! ind = randperm(size(G,1)); G = G(ind, ind); for i=1:length(fn) meta.(fn{i}) = meta.(fn{i})(ind); end % Plot adjacency matrix (unsorted) figure('name', 'Adjacency matrix (unsorted)') spy(G); xlabel(labels{2}) ylabel(labels{1})
Find overlapping communities
p = 2; % Number of communities niter = 20000; % Number of iterations [degree_correction, community_affiliation, community_detection] = overlapping_community_detection(G, p, niter);
----------------------------------- Start initialisation of the MCMC algorithm for CGGP ----------------------------------- End initialisation ----------------------------------- ----------------------------------- Start MCMC for undirected CGGP graphs Nb of nodes: 1224x1224 - Nb of edges: 16715 (0 missing) Nb of chains: 1 - Nb of iterations: 20000 Estimated computation time: 0 hour(s) 3 minute(s) Estimated end of computation: 01-Feb-2020 17:39:25 ----------------------------------- Markov chain 1/1 ----------------------------------- i=2000 alp=4886.52 sig=-1.095 tau=3.37 a=0.25 0.22 b=0.71 0.82 w*=0.24 0.18 b2=2.38 2.76 alp2=1289.99 rhmc=0.70 rhyp=0.31 eps=0.026 rwsd=0.053 i=4000 alp=5582.58 sig=-1.206 tau=2.89 a=0.22 0.19 b=0.97 0.83 w*=0.25 0.16 b2=2.81 2.40 alp2=1553.58 rhmc=0.50 rhyp=0.23 eps=0.029 rwsd=0.055 i=6000 alp=5337.33 sig=-1.266 tau=2.48 a=0.20 0.18 b=0.97 1.08 w*=0.32 0.26 b2=2.41 2.67 alp2=1687.70 rhmc=0.90 rhyp=0.22 eps=0.013 rwsd=0.057 i=8000 alp=4691.75 sig=-1.229 tau=2.39 a=0.22 0.18 b=1.13 0.95 w*=0.48 0.25 b2=2.70 2.27 alp2=1603.53 rhmc=0.94 rhyp=0.23 eps=0.013 rwsd=0.057 i=10000 alp=5270.29 sig=-1.298 tau=2.43 a=0.20 0.17 b=1.10 0.92 w*=0.21 0.16 b2=2.67 2.22 alp2=1664.29 rhmc=0.94 rhyp=0.22 eps=0.013 rwsd=0.057 i=12000 alp=4878.96 sig=-1.349 tau=2.09 a=0.20 0.18 b=1.35 1.25 w*=0.23 0.25 b2=2.82 2.62 alp2=1804.06 rhmc=0.94 rhyp=0.21 eps=0.013 rwsd=0.057 i=14000 alp=4490.11 sig=-1.390 tau=1.97 a=0.21 0.18 b=1.50 1.33 w*=0.26 0.24 b2=2.95 2.61 alp2=1754.57 rhmc=0.94 rhyp=0.23 eps=0.013 rwsd=0.057 i=16000 alp=5801.94 sig=-1.476 tau=2.04 a=0.19 0.16 b=1.86 1.43 w*=0.29 0.24 b2=3.79 2.91 alp2=2032.93 rhmc=0.94 rhyp=0.21 eps=0.013 rwsd=0.057 i=18000 alp=5696.85 sig=-1.627 tau=1.82 a=0.20 0.15 b=2.03 1.56 w*=0.26 0.30 b2=3.69 2.83 alp2=2149.65 rhmc=0.94 rhyp=0.22 eps=0.013 rwsd=0.057 i=20000 alp=3738.35 sig=-1.515 tau=1.52 a=0.20 0.17 b=2.30 1.77 w*=0.27 0.19 b2=3.50 2.70 alp2=1976.00 rhmc=0.94 rhyp=0.22 eps=0.013 rwsd=0.057 ----------------------------------- End MCMC Computation time: 0 hour(s) 2 minute(s) ----------------------------------- ----------------------------------- Start parameters estimation for CGGP graphs: 500 samples Estimated end of computation: 01-Feb-2020 17:40:17 (0.0 hours) |---------------------------------| |*********************************| End parameters estimation for CGGP graphs Computation time: 0.0 hours -----------------------------------
Some plots
% Identify each feature as liberal or conservative using ground truth % (This step would normally require a human interpretation of the features) [~, ind_features] = sort(median(community_affiliation(meta.isright,:), 1)./median(community_affiliation, 1)); featnames = {'Liberal', 'Conservative'}; % Name of the interpreted features % Print classification performance with ground truth [confmat] = print_classif(fullfile('./', ['classif_' num2str(p) 'f.txt']), ... community_detection, meta.groups, ind_features, label_groups);
Classification performance ========================== Confusion matrix (counts) ------------------------- Group : Feat 1 Feat 2 | Total Left : 532 56 | 588 Right : 27 609 | 636 Total : 559 665 | 1224 ------------------------- Confusion matrix (%) ------------------------- Group : Feat 1 Feat 2 | Total Left : 43.46 4.58 | 48.04 Right : 2.21 49.75 | 51.96 Total : 45.67 54.33 |100.00 ------------------------- Group assignments of features ------------------------- Feat 1: Left Feat 2: Right ------------------------- Accuracy = 93.22 Error = 6.78 ==========================
% Plot levels of affiliation to each community for a subset of blogs color = [0 0 .8; .8 0 0]; names = {'blogsforbush.com' 'instapundit.com' 'drudgereport.com' 'tagorda.com' 'danieldrezner.com/blog' 'andrewsullivan.com' 'iwantmycountryback.org' 'democraticunderground.com' 'wonkette.com' 'washingtonmonthly.com' 'dailykos.com' 'atrios.blogspot.com'}; ind = zeros(size(names,1),1); lab = cell(size(names,1), 1); for i=1:size(names,1) ind(i) = find(strcmp(meta.name, names{i}) & strcmp(meta.name, names{i,1})); lab{i} = sprintf('%s (%s)', names{i}, label_groups{meta.groups(ind(i))}(1)); end plot_nodesfeatures(community_affiliation, ind, ind_features, lab, featnames, color);
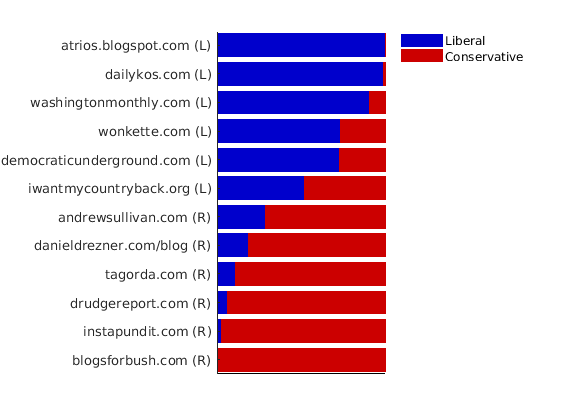
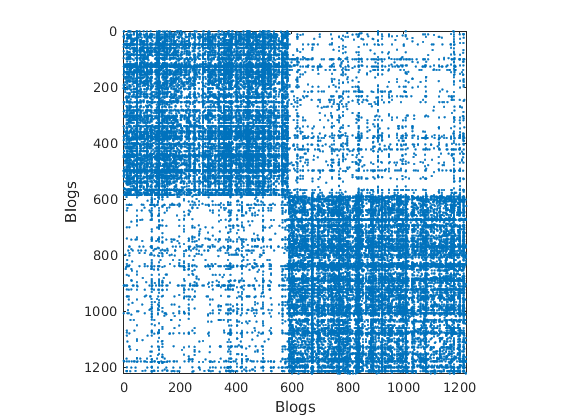
% Plot the graph by clustering the nodes by community with maximum level of affiliation to see block structure
plot_sortedgraph(G, community_detection, community_detection, ind_features, labels);